Pengertian Matriks
Matriks adalah kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks.
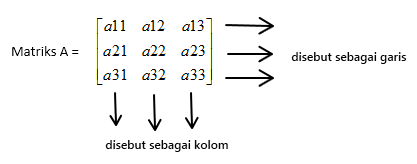
Elemen/anggota matriks,
a11 = terletak pada baris pertama dan kolom pertama
a12 = terletak pada baris pertama dan kolom kedua
a13 = terletak pada baris pertama dan kolom ketiga
dst....... (angka didepan melambangkan baris dan angka dibelakang melambangkan kolom)
Ordo Matriks
Dijelaskan sebelumnya matriks terdiri dari unsur-unsur yang tersusun secara baris dan kolom. Jika banyak baris suatu matriks adalah m, dan banyak kolom suatu matriks adalah n, maka matriks tersebut memiliki ordo matriks atau ukuran m x n. Perlu diingat bahwa m dan n hanya sebuah notasi, sehingga tidak boleh dilakukan sebuah perhitungan (penjumlahan, perkalian).
- Banyak baris, m = 3
- Banyak kolom, n = 3
- Ordo matriks, m x n = 3 x 3
Contoh lain
- Banyak baris, m =4
- Banyak kolom, n =2
- Ordo matriks, m x n = 4 x 2
Jenis-jenis Matriks
Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut
1. Matriks Baris dan Matriks Kolom
A = (1 4) atau B = (3 7 9) adalah matriks baris
2. Matriks Persegi
Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi.
adalah matriks persegi berordo 3x3, atau
3. Matriks Segitiga Atas dan Segitiga Bawah
adalah matriks segitiga atas,
adalah matriks segitiga bawah.
4. Matriks Indentitas
Hampir sama dengan matriks skalar, tetapi untuk identitas metriks diagonalnya selalu angka satu
5. Matriks Diagonal
atau
6. Matriks Skalar
Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
atau

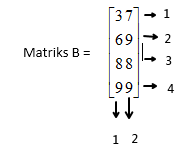

No comments:
Post a Comment