Pengertian Pertidaksamaan Rasional
Pertidaksamaan merupakan kalimat matematika terbuka yang menggunakan sebuah tanda > (lebih dari), < (kurang dari) ≤ (kurang dari atau sama dengan) dan ≥ (lebih dari atau sama dengan).
Bentuk – Bentuk Umum Pertidaksamaan Rasional
Berikut ini adalah beberapa bentuk umum dari pertidaksamaan rasional :
Ketentuan yang tidak boleh dilakukan:
1. Mencoret fungsi ataupun faktor yang sama pada pembilang dan penyebut
Untuk menyelesaikan himpunan pertidaksamaan rasional dapat ditentukan dengan mengunakan langkah-langkah sebagai berikut :
- Himpunan kita nyatakan kedalam bentuk umum.
- Tentukan pembuat nol pada pembilang dan penyebutnya.
- Tulis terlebih dahulu pembuat nol pada garis bilangan dan tentukan tanda untuk tiap-tiap interval pada garis bilangan.
- Tentukan daerah penyelesaian yakni untuk pertidaksamaan “>” atau “≥” daerah penyelesaian berada pada interval yang bertanda positif dan untuk pertidaksamaan “<” atau “≤” daerah penyelesaian berada pada interval yang bertanda negaitf.
- Dengan memperhatikan syarat bahwa penyebut tidak sama dengan nol, tulis himpunan penyelesaian yaitu interval yang memuat daerah penyelesaiannya.
Contoh Soal :

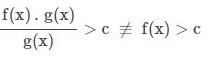



No comments:
Post a Comment